First Program

The First Program

Note that in the Baby and Mark 1 environment binary was written out with least significant bit first. The Baby instruction codes are as follows, given CI is the current control address, A is the Accumulator, and S is the contents of a store address (also see the Baby specification):

000 CI = S	010 A = - S	001 A = A - S	011 If A < 0, CI = CI + 1
100 CI = CI + S	110 S = A	101 A = A - S	111 HALT

The first program was written by Tom Kilburn. It was a program to find the highest proper factor of any number a; this was done by trying every integer b from a-1 downward until one was found that divided exactly into a. The necessary divisions were done not by long division but by repeated subtraction of b (because the "Baby" only had a hardware subtractor).

The original number used was quite small, but within a few days he had built up to trying the program on 2¹⁸; here around 130,000 numbers were tested, which took about 2.1 million instructions and involved 3½ million store accesses. The correct answer was obtained in a 52 minute run (in detail ..).

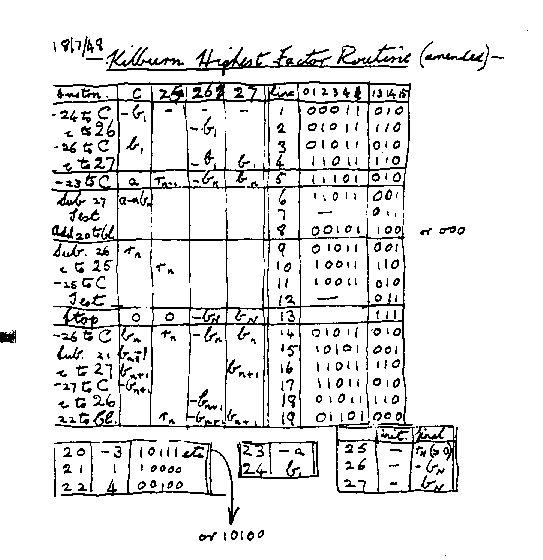
The original program has been lost, but the Tom Kilburn and Geoff Tootill have reconstructed the first program for the 50th Anniversary celebrations. The revised version (above) is from G.C Tootill's notebook, Tom Kilburn's assistant.

In this version, C is used to represent the accumulator A, and a, b, r respectively the number for factorizing, a trial factor and a remainder. The control register CI is referred to on lines 8 and 19. Line 8 jumps back to line 6 (after 1 has been added to CI) thus closing the inner loop of repeatedly subtracting b from the accumulator until it goes negative, and line 19 jumps back to line 5 to reset the accumulator to a before the repeated subtraction of the next lower b. You can see that in fact separate store locations were used to store both positive and negative current values of both a and b, and in fact a-1, the initial value of b, is held rather than a (the usage is: 23 -a, 24 a-1, 26 -b, 27 b).

The original program was encoded in only 17 instructions. The revised version includes two extra instructions to facilitate rerunning the program with the same number (in detail ...). This was a sensible thing to do until the basic reliability of the Baby had been demonstrated.