![[*]](crossref.png) .]
.]
It is possible by setting certain switches to arrange that the machine `stops' when certain instructions are reached. This is effected by arranging that these instructions have no completion signals. The instructions in question are /L and /G. Each of these can be independently made either a `time wasting instruction' or a stop.
Dummy stops are very useful in testing routines. The programmer is
recommended to insert them at points where major operations may be
considered complete. [Note that a /L dummy stop is included in
the ``routine changing sequence'', which brings subroutines into
electronic storage from the drum; see p. ![[*]](crossref.png) .]
.]
When an instruction with function symbol /V is obeyed an impulse is applied to the diaphragm of a loudspeaker. By doing this repeatedly and rhythmically a steady note, rich in harmonies, can be produced. This is used to enable the operator to be called to attend to the machine in some way. The simplest case is where the whole of a job is completed and it is required to clear the electronic stores and start something different. All that is then required is to repeat a cycle of instructions including a hoot, e.g.
One can set up a row of twenty digits on twenty switches. This row
`H' can affect the behaviour of the machine through instructions with
function symbol // or /Z. The former of these will be
discussed under magnetic transfers. The latter is used for putting
small pieces of information into the machine by hand. [The equations
for /Z are
![]() ,
,
![]() .] Suppose for example that we
have a routine for calculating some function of a four character line,
and suppose that the calculation takes five minutes. It would then be
reasonable to put the arguments in through the switches. This would
be particularly so if the arguments used depend partly on the judgment
of the experimenter and partly on the values recently obtained,
e.g. if one were trying to find a zero of the function, but one was
not wishing to repeat the process often enough to mechanise it fully.
Again if one were playing chess against the machine this would be the
natural way of registering one's moves. [These are allusions to two
of Turing's own projects -- his very early work on machine chess, and
his project to investigate the zeros of the Riemann zeta function.]
(See also the `formal mode', pp.
.] Suppose for example that we
have a routine for calculating some function of a four character line,
and suppose that the calculation takes five minutes. It would then be
reasonable to put the arguments in through the switches. This would
be particularly so if the arguments used depend partly on the judgment
of the experimenter and partly on the values recently obtained,
e.g. if one were trying to find a zero of the function, but one was
not wishing to repeat the process often enough to mechanise it fully.
Again if one were playing chess against the machine this would be the
natural way of registering one's moves. [These are allusions to two
of Turing's own projects -- his very early work on machine chess, and
his project to investigate the zeros of the Riemann zeta function.]
(See also the `formal mode', pp. ![[*]](crossref.png) -
-![[*]](crossref.png) ).
).
In the calculation of logarithms, reciprocals and square roots it is
desirable to be able to `standardize' numbers i.e. to express them in
the form ![]() where
where
![]() . This is made
possible at high speed by the use of instructions with the function
symbol /@.
. This is made
possible at high speed by the use of instructions with the function
symbol /@.
[This instruction also has cryptographic applications which Turing does not mention, but which he would have known very well from his work at Bletchley Park, which was then still very secret. Cryptography is also a significant application of the /R function symbol, which counts the number of one bits in a word; Turing refers to this as the ``sideways adder'' in his quick-reference summary, but does not refer to the instruction at all in the main text of the manual. The relevant equations are:
| Function symbol | Equations |
| /R |
|
| /@ |
|
Ifand, then
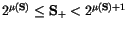
If, then
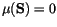
In the Mark II machine the principle that the state of the machine at one completion signal determines the state at the next is abandoned if instructions with function symbol /W are used. The behaviour of the machine is then to be described as a `stochastic' (i.e. chance-controlled) process and is suitable for calculations concerned with stochastic processes. The instruction /W actually puts random digits into the twenty least significant digits of the accumulator.
The following problem is suitable for the use of this facility.
A man in New York starts walking from a street intersection, and at each street intersection decides in which direction to walk by twice tossing a coin (each of the four directions is chosen equally often). It is required to find the probability that before walking twenty blocks he will have succeeded in returning to his starting point. For this purpose New York is to be assumed to be an infinite rectangular lattice of streets and avenues.
The quantity Z is a twenty digit line which is intended to indicate
the time. If ![]() and
and ![]() are the contents of Z at two times
are the contents of Z at two times
![]() and
and ![]() , measured in seconds, then
, measured in seconds, then
[Instructions with function symbol /Y set the low 20 digits of
![]() to Z.]
to Z.]
We mentioned on p. ![[*]](crossref.png) that an extra identification line
was added to each magnetic page and that there is a corresponding line
on each tube. The only significant effects of these lines are
that an extra identification line
was added to each magnetic page and that there is a corresponding line
on each tube. The only significant effects of these lines are
![[*]](crossref.png) ),
),
![[*]](crossref.png) .
.
[Three branch introductions have been introduced so far -- the
unconditional /P, the A-conditional /H and the
B-conditional /T. These are all absolute branches, setting
![]() if the branch is taken. They have relative variants,
/Q, /M and /O respectively, which are identical
in their effects except that if the branch is taken, we have
if the branch is taken. They have relative variants,
/Q, /M and /O respectively, which are identical
in their effects except that if the branch is taken, we have
![]() .]
.]
The machine is synchronised by an oscillator with a frequency of 100
kc/s. One cycle (occupying 10 ![]() s) of this oscillator may be
called a `digit period'. These digit periods determine the most
fundamental rhythm of the machine, but there is another almost equally
important rhythm, in which time is divided into `beats' of 24 digit
periods. Four of these periods form what is called the `blackout
period' of the beat. The remaining twenty are used for operations on
twenty digit rows, each digit being dealt with in one digit period.
The `prepulses' or `completion signals' occur in the blackout periods,
and are separated by integral numbers of beats, i.e. by multiples of
240
s) of this oscillator may be
called a `digit period'. These digit periods determine the most
fundamental rhythm of the machine, but there is another almost equally
important rhythm, in which time is divided into `beats' of 24 digit
periods. Four of these periods form what is called the `blackout
period' of the beat. The remaining twenty are used for operations on
twenty digit rows, each digit being dealt with in one digit period.
The `prepulses' or `completion signals' occur in the blackout periods,
and are separated by integral numbers of beats, i.e. by multiples of
240 ![]() s. As has been mentioned (p.
s. As has been mentioned (p. ![[*]](crossref.png) ) some
instructions overlap their successors, but for programming purposes
one may take it that the time consumed in an instruction is that
dividing the prepulse initiating it with that initiating its
successor. The numbers of beats for each instruction are shown on p.E
[in the appendices]. The times for the magnetic instructions are
mentioned under the heading of the magnetic wheel.
) some
instructions overlap their successors, but for programming purposes
one may take it that the time consumed in an instruction is that
dividing the prepulse initiating it with that initiating its
successor. The numbers of beats for each instruction are shown on p.E
[in the appendices]. The times for the magnetic instructions are
mentioned under the heading of the magnetic wheel.