

Published in Journal of Molecular Graphics & Modelling, 19, 623-627 (2001)
Huw O. Pritchard, Distinguished Research Professor Emeritus
Department of Chemistry, York University, Toronto, Canada M3J 1P3
huw@yorku.ca
To mark half a century of computational quantum chemistry, this account recalls some computer experiments in Manchester, 1951-1960
" ... whether we last the night or no,
I'm sure it's always touch and go."
Dylan Thomas, "Eli Jenkins' Prayer"
The Manchester University--Ferranti Mk I computing machine became available for experimentation by academic users in the middle of 1951. That October, Frank Sumner began his Ph.D. study under the supervision of Christopher Longuet-Higgins to explore of what use this machine might be in Chemistry. His project was, initially, to solve the Hückel molecular orbital eigenvalue problem for some aromatic hydrocarbons by using the contour integration methods of Coulson and Longuet-Higgins.1 Longuet-Higgins' antipathy towards computers in chemistry at that time is well known,2a the gist being that a solution of the Schrödinger equation, either as a set of numbers or as an algebraic series (such as those of Hylleraas for He or of James and Coolidge for H2), could not possibly provide the same insight into atomic and molecular structure as one could derive from an orbital picture;2b hence, I suspect that this initiative came from M. G. Evans.
Within a few months, Longuet-Higgins left for a Chair of Theoretical Physics in London, and shortly thereafter for one in Theoretical Chemistry in Cambridge. Meanwhile, Frank Sumner, without guidance and finding his project intractable, came to me and asked if I would help; he provided me with a big fat Programmer's Manual and we got down to it together. Lacking much progress, we soon sought help from Alan Turing and Tony Brooker in the Computing Machine Laboratory and they advised us, rightly of course, to forget the contour integrals and attack the eigenvalue problem head-on.
It seemed obvious at the time that we should make use of symmetry in order to reduce the sizes of the secular determinants that we wished to solve, but this led to the determinants being unsymmetric. Brooker was writing a Lanczos algorithm to reduce a matrix to its characteristic polynomial,3 so we adopted this approach to get the eigenvalues, and then generated the eigenvectors by iterative procedures, such as the Rayleigh quotient method. Much later, when the Givens, and then the Householder methods matured, it became clear that it was faster not to factorise the matrices in this way, but keep everything symmetric and solve the full matrix for both its eigenvalues and eigenvectors; here, again, Brooker pointed us towards one of the standard avenues for solving the eigenvalue problem.4
The Ferranti Mk I machine could do about 800 integer operations per second; floating point operations -- multiplication, division, square roots, etc., were by subroutine, about 10 per second. The machine was built mainly from about 4050 glass radio valves, housed in the usual array of racks in a room of about 20 feet by 30 feet; off to the back was the control room, into which we never went, housing the power supplies and the 25 kW cooling system required to dissipate the heat from the electron-tube filaments.
The `fast store' consisted of 8 Williams-type cathode ray tube (CRT) storage devices, each capable of holding 64 20-bit data strings. An individual data string could represent an instruction, 10 bits for the operand address and 10 bits for the operation, or an integer number; alternatively, two consecutive strings could be taken together to represent a floating point number, 30 bits for the mantissa (including a 1-bit sign) and 10 bits for the exponent and its sign. Another storage tube held eight 10-bit counters, the value of any of which could be complemented with the address part of an instruction so as to select consecutive elements of a vector or matrix. And a `backing store' consisted of a rotating magnetic drum, capable of holding 16K 40-bit words, with an access time of 35 ms for read and 90 ms for write.
One other trick that is now just a curiosity was the method of generating random numbers: the signal from a noisy resistor was chopped into zeros and ones and squared a couple of times, thus yielding truly random numbers.
The console consisted of a large desk with a 5-hole paper tape reader (200 characters per second) and paper tape punch (15 cps) on one side, and an electric typewriter (6 cps) on the other; the much faster `golf-ball' IBM Selectric typewriter was still in the future. In between was a console with four 3-inch CRTs displaying the contents of the accumulator, the two registers and the eight counters, and two 6-inch CRTs into which contents of any two of the eight storage tubes could be copied for observation -- or manipulation by hand! These displays consisted of two columns of 32 20-bit strings, together with one extra 20-bit string to tell you which tube you were seeing; these strings were subdivided into 4 x 4 blocks for easy viewing -- see Figure 1 in which the bright dots are ones and the feint ones are zeros.5 Each of the 5-bit sub-strings was named after the corresponding teleprint character of the 5-hole tape, except for the teleprint control characters e.g. carriage return, etc., to which non-alphabet symbols were assigned. The use of the teleprint code to represent the numbers 0-31, and in which to write algorithms was much reviled by some programmers,6a but I can still recite it by heart,
/E@A:SIU½DRJNFCKTZLWHYPQOBG"MXV£almost as well as my ABC.


Figure 1. (a) Photograph of a Kilburn--Williams cathode ray storage tube showing the contents of storage locations (left-hand side) // to £/, a segment containing instructions, and (right-hand side) /E to £E, comprising constants, work space and addressing information; (b) alphabetic representation in `Coding Sheet' form. (Adapted from the Programmer's Handbook, 1952 Edition).
In front of the display tubes were various switches by which instructions could be performed one at a time, and two banks of 20, one for setting up a string to write into the store, and another for an instruction to perform, which could include either writing in the hand-switches or performing some other operation. `Finger trouble' -- as Brooker called it6b -- was a frequent malady.
Machine time was allocated in half-, one-, two-, and four-hour slots during the day, with a (nominal) 8-hour slot from midnight on; the time from 7.30-9.00 a.m. was engineering time, in which the engineers would run tests, make small modifications, and look for failing valves by turning up the filament voltages to check for low emission. Otherwise, with an estimated filament lifetime of about 5000 hours,5 one would anticipate random failures about every 75 minutes. Soon, a pattern was established whereby we received one half-hour and one 8-hour slot per week, the former for `development' and the latter for `production'. Other overnight regulars were the Weather Service, TNPG (The Nuclear Power Group) and A. V. Roe (designing the Vulcan Bomber, I would guess). During the night, there was one full time engineer on duty, and with him asleep in the corner in an arm chair, there was little to do except to watch the dots as the calculation progressed. Each 20-bit instruction became highlighted as it was accessed, so you could watch the machine sweep through them, knowing exactly where you were, or else watch the numbers as they kept on changing.
We knew little about convergence at that time, and so would plant two numbers (one the convergence criterion and the other the current value to be tested) in the bottom right-hand corner of one of the storage tubes. Often the one would approach the other monotonically, and the calculation progressed. However, sometimes the test number would begin to oscillate, and for which a solution had been provided. There were two switches up on the right-hand side, labelled L and M, and if you put an instruction in the loop ending in /L or /M, it would read the corresponding switch and if it was up, the programme would either stop so that you could fiddle with the hand-switches, or it could be made to come out of the loop and carry on to the next step. With our `large' matrices, of order 8-10, one might get a converged eigenvalue and eigenvector perhaps twice an hour towards the end (when there were more and more vectors against which to orthogonalise the present one), so any result was better than no result as it could always be worked upon later to try to improve it. Frequently, with the low soporific hum, drowsiness would win, only to be broken by the typewriter motor, which switched itself off after 5 minutes of inactivity, starting up to signify that another result was about to arrive.
One's relief at this modest success can be gauged by two statements from
the Programmer's Handbook. In the 1952 Edition:
"It should be clearly understood that the machine is liable to carry
out certain operations incorrectly. This malfunctioning can either be
chronic or transient. Whilst everything is being done on the engineering
side to eliminate these undesirable features, nevertheless in the meantime
programmers are obliged to minimise the effects of machine errors by devices
in the programme."
Then follows some advice on recognising the possible types of errors,
on breaking the programme up into `steps', and on incorporating some
consistency tests, if possible, within each step. And, from the 1953 Edition
(when the machine was working rather more reliably):
"... The duration of such steps depends on how the machine is behaving,
but programmers must be prepared to arrange for steps as small as 1 minute.
If the machine is functioning well, however, then fault-free runs of up to
½ hr can be relied on."
Also, listed daily on the notice board was a table of the magnetic tracks that were thought to be unreliable: this meant that all programmes had to be written in a relocatable form, and the storage tracks to be avoided had to be entered, either by paper tape or via the hand-switches, before starting a given run.
When a bad track was encountered, or a documentable fault occurred, there was a log book into which the event was entered,6b and by 1956, the machine would often run for a full 24 hours without an entry being made. It is remarkable, now, to think that this machine could do about 68 million integer instructions in 24 hours, slightly more than a long-since obsolete Intel 486 processor could do in 1 second!
Often, while staring at the monitors, usually at about 4 a.m., bits (`clods' in Turing parlance) would drop into or out of the corners of the CRT display; not surprising, since the machine had been running by then for about 18 hours. Time to wake up the engineer! Depending upon the severity of the fault, you would either hang around for a while, or else abandon proceedings for the night. If I had a 9.30 lecture, I would find something to do in the lab: at that time, we were involved in radioactive counting, and it is remarkable how much lower the background counts were at 4 in the morning -- but the Greats of the Physics Department one block over in Coupland Street had known that decades before. If not, I would go home to sleep.
Of course, when one finished, nothing could be left on the machine. Numbers required for future use were punched out on paper tape -- twice: you then held them up to the light, and if they were the same, all well and good. If not, one could usually reconstruct the correct data from the printed record and the two tapes; without a printed record (sometimes the printer did not work), you punched a third tape and created the data tape for the next session on the principle that lightning never strikes twice in the same place.
Through these methods, we were able to calculate the eigenvalues and eigenvectors of Hückel determinants for polybenzenoid hydrocarbons up as far as ovalene, 30 carbon atoms7a (although this paper was actually preceded by one relating to the properties of a homologous series of Hückel-style secular determinants, with the algebraic analysis provided by Alan Turing).8 That we did not go further was not due to lack of fortitude, but the size of vector that we could handle was limited by the page size of 32 numbers; to add another ring would have made it 34 carbon atoms, which was too many. Also, procedures were limited to 128 20-bit instructions, beyond which a cumbersome `Routine Changing Sequence' had to be invoked. In fairly quick succession, we examined bond-order--bond-length relationships for naphthalene and anthracene,9 and the combination of force fields with Hückel energies to treat steric hindrance and twisting in o, o'-substituted biphenyls,10 a bit like what is now done in Molecular Mechanics. We tried to extend our methods to heteroaromatics, but the main value of that paper was to introduce for the first time the modern interpretation of electronegativity as the derivative of the orbital electronic energy with occupation number.7b It is interesting to note that Robert Mulliken never associated11 his formula for electronegativity, (I + E)/2, with the slope of a parabola at the middle of three unit-spaced co-ordinates, even though the parabolic nature of electronic binding energies in many-electron atoms had been recognised in the late 1930s.
Then, by 1955, as far as Hückel-type molecular orbital calculations were concerned, we were stuck, limited by the size of the storage space and by the intrinsic speed of the machine. So, with a new student, Brian Gray, we looked around for other things that we might do. We tried a calculation of the dipole moment for a diatomic,12 and went on to examine infra-red absorption intensities, finding that it was quite possible for an overtone to be more intense than the fundamental.13 However, our main effort was devoted to finding how many linear combinations were needed to give an acceptable representation of the wave function of a diatomic molecule, a simple one of course, H2+.14 We limited ourselves to 10 hydrogen-like atomic orbitals, 1s to 4f inclusive; this required the calculation of 165 two-centre integrals, which could not possibly have been done with suffcient speed and accuracy by numerical quadrature because they were functions of two variables. We devised a method by which the the orbital functions could be represented symbolically in the machine and the integrals were calculated by algebraic manipulation before finally being reduced to a number for the particular value of R, the internuclear distance in question; unbeknownst to us, S. F. Boys was doing a very similar thing at about the same time, in Cambridge.15 Since then, the use of symbolic algebra in Computational Chemistry has been slow in coming. Longuet-Higgins' fears that we might be inundated by massive polynomial solutions of the Schrödinger equation have not materialised, such solutions being limited to rather restricted kinds of potential functions,16 at least so far. However, the calculation of two-centre integrals symbolically has, just recently, reached an elegantly viable level.17
The answer to our original question was that if the basis functions were chosen from a complete set, one on each nucleus, 10 functions were enough to give the total energy of H2+ correct to within 2 x 10-5 Hartree.18
Around 1956, two major advances occurred: Brooker introduced a compiler known as Autocode,19 which simplified enormously the programming of small one-off calculations, and a new machine, the Ferranti Mercury, was commissioned a year later. It was a little over an order of magnitude faster, it made fewer mistakes, and had a superior Autocode that made the recursive calculation of Morse wave functions and the like quite straightforward. Demand expanded to fill the new capability, and within a month, machine time was at a premium again. Nevertheless, we continued to hold on to our one half-hour and one overnight weekly allocation.
I will conclude by recounting just two episodes from this later period. One night, I was alone, the engineer having failed to show up for the midnight shift. Around 3.30 in the morning, I began to smell warm insulation, and as it got stronger, I phoned the backup engineer at home, who decided that the power should be switched off. However, the control room was locked, and by the time he arrived, smoke was emanating from one of the electronic cabinets. The machine was out of action for a whole week.
Early in 1960, a 3-inch CRT with 35 mm camera was incorporated into the system, and we tried to use it to plot wave functions. We soon found that unit displacement in the x-direction was about 30% longer than in the y-direction, and dragged the Electrical Engineering faculty member who had built it, Richard Grimsdale, away from his lunch to adjust it for us. It had only been built as a kind of a toy, and was placed in a rack about 6 inches above the floor. So Frank Sumner and I lay at on our stomachs, holding a ruler up to the face of the CRT until 1 unit displacement in either direction had been adjusted to be the same -- as far as we could tell. Grimsdale was most contemptuous of our attempt to wring more precision out of the device than had been intended, but we were able to publish several satisfactory pictures of wave functions,18,20 with a spot size of about 1 mm, i.e. a resolution of about 25 dots per inch! Two unpolished examples are shown in Figures 2 and 3.

Figure 2. A 35 mm film strip showing Morse wave functions for the 15 vibrational levels of H2 over the range -0.6 < (r-re) < 4.4 Angstrom; the final composite diagram is Figure 1 of Reference 20.
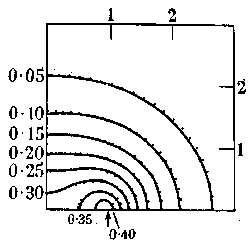
Figure 3. Photographic superposition of contours for an approximate wave function for the ground state of H2+ (dots) on hand-drawn contours for the exact wave function, taken from Reference 21; the completed diagram is Figure 1 of Reference 18.
Finally, H2+ has a place in the annals of computer technology. When the concept of a one-level store (now more commonly referred to as virtual memory) was invented, Brooker and Sumner used our 10th order [H - SE] (Z = 1) matrix with which to prove its validity.22
Frank Sumner recently retired as Professor of Computer Science in Manchester, and Brian Gray as Professor of Mathematics in Sydney. In addition, one other person, Brian Sutcliffe, became involved towards the end of 1959. He was doing his Ph.D. with Roy McWeeny in Keele, but Keele did not yet have authority to grant Ph.D. degrees, so I became his (nominal) supervisor. He came up to Manchester once a week to do atomic structure calculations on the Mercury machine, and used a small corner of my office as a base, gaining his Manchester Ph.D. in 1962; he recently retired also, as Professor of Theoretical Chemistry in York (England).
References